I have been using the WGCNA package (https://labs.genetics.ucla.edu/horvath/CoexpressionNetwork/Rpackages/WGCNA/faq.html) for correlation networks.
http://bmcbioinformatics.biomedcentral.com/articles/10.1186/1471-2105-9-559
I understand what a hard threshold is: absolute value of correlation matrix, choose a cutoff (e.g. 0.85), anything above is considered connected in the network. But then there is soft thresholding which is when you exponentiate the correlation matrix and that accentuates larger connections.
How do you then decide which ones are connected or not? Do you do a hard threshold after the soft thresholding?
Basically, going from `|correlation|` => `exponentiated(correlation)` => `adjacency_matrix`
`One potential drawback of soft thresholding is that it is not clear how to define the directly linked neighbors of a node. A soft adjacency matrix only allows one to rank all the nodes of the network according to how strong their connection strength is with respect to the node under consideration. If a list of neighbors is requested, one needs to threshold the connection strengths, i.e. the values in the adjacency matrix. When dealing with an unweighted network, this is equivalent to the standard approach of hard thresholding the co-expression similarities since the adjacency function is monotonically increasing by definition.`
https://labs.genetics.ucla.edu/horvath/GeneralFramework/WeightedNetwork2005.pdf
Can you change the hard threshold for the soft threshold or is that hard-coded in there? If so, what is that threshold?


Thanks @Lluis! I understand the concept of exponentiating the correlation matrix but I am still confused how `WGCNA` determines which genes/nodes are connected in the network. For example, if one had a correlation of `0.99**12 = 0.886` what happens to that value? Is there a hard threshold underlying the soft threshold?
Well usually the steps are: correlation->adjacency (cor**power)->Topological Overlap Measure (That takes into account the correlation between the other genes to asses how much two genes are correlated, see) -> clusters (with the DynamicTree algorithm). It is in this last step that the clusters are created, see. There is a hard threshold on the DynamicTree process, but it is the number of genes involved on each module.
Thanks again for the response Lluis. Shouldn't TOM have the threshold since it needs to count the shared neighbors?
TOM calculation counts neighbors using a weighted sum: the weaker the connection, the less it counts.
Hi Peter, Is that a `signed TOM`? My understand of TOM is that for `node_A` and `node_B` it takes the overlap of neighbors for `node_A` and `node_B` then normalizes. By weighted, do you mean the weights of each neighbor are taken into account when saying if 2 nodes have an overlap of neighbors? So in the end, everything is connected (either strongly or loosely)? Are there still cutoffs during this part either?
See slide 13 of this presentation, about the meaning of weighted network and their relationship with thresholds. By weight is understood that the relation between node_A and node_B can be between -1 and 1 (or in any continuous range), not 1 or 0 by yes or not connected, which would be an unweighted network, like DE analysis, or a network of people I know. So yes, everything is connected or at least we can calculate a correlation between everything. Cutoffs are not needed to create the TOM matrix.
I'm about ready to select this as the correct answer. Thanks again for your time Lluis in helping me understand this. Just to clarify, during the TOM calculation of a weighted network, is that a signed TOM. And lastly, is the `nearest neighbors` calculation in a network (getting actual nodes that are connected) irrelevant in a weighted network?
TOM in a weighted network can be signed or unsigned. Whether it is signed or unsigned has nothing to do with whether the network is weighted or unweighted.
Nearest neighbors of a node (call the node A) can be generalized in a weighted network to those nodes that have the highest connection strength to node A. It could be relevant in some analyses (network neighborhood analysis).
Can't thank you and Lluis enough for helping me get the details of all of this. Great tool Peter!
Signed TOM takes into account that some genes may have an unclear signal of correlation between some genes. It is explained in the technical paper you link but the idea is that a gene A may be positive correlated to gene B and C but between gene B and C there is a negative correlation. So how can it be A positive correlated to both B and C? => the signal/pattern is not clear. If you perform an unsigned TOM, it doesn't care about such noise and the resulting modules would be less correlated. You can calculate the TOM matrix with both signed or unsigned approach.
Well, it is almost never irrelevant, the whole point of this technique is to identify how the network of genes work, how do they work together, and with which genes work together. Thus defining which are the nearest neighbors is fundamental. In other ways, people is trying to achieve that by looking into which proteins interact, which transcription factors repress other genes... However, this neighbors (genes in the same module) are further explored with enrichment analysis, to asses if they are really meaningful, from a biological point of view.
It is also helping me to realize things, and to learn how to explain it, as well as checking I don't say things different than Peter, one of the authors of WGCNA.
https://labs.genetics.ucla.edu/horvath/GeneralFramework/WeightedNetwork2005.pdf
Can you change the hard threshold for the soft threshold or is that hard-coded in there? If so, what is that threshold?
Dear Lluís Revilla Sancho
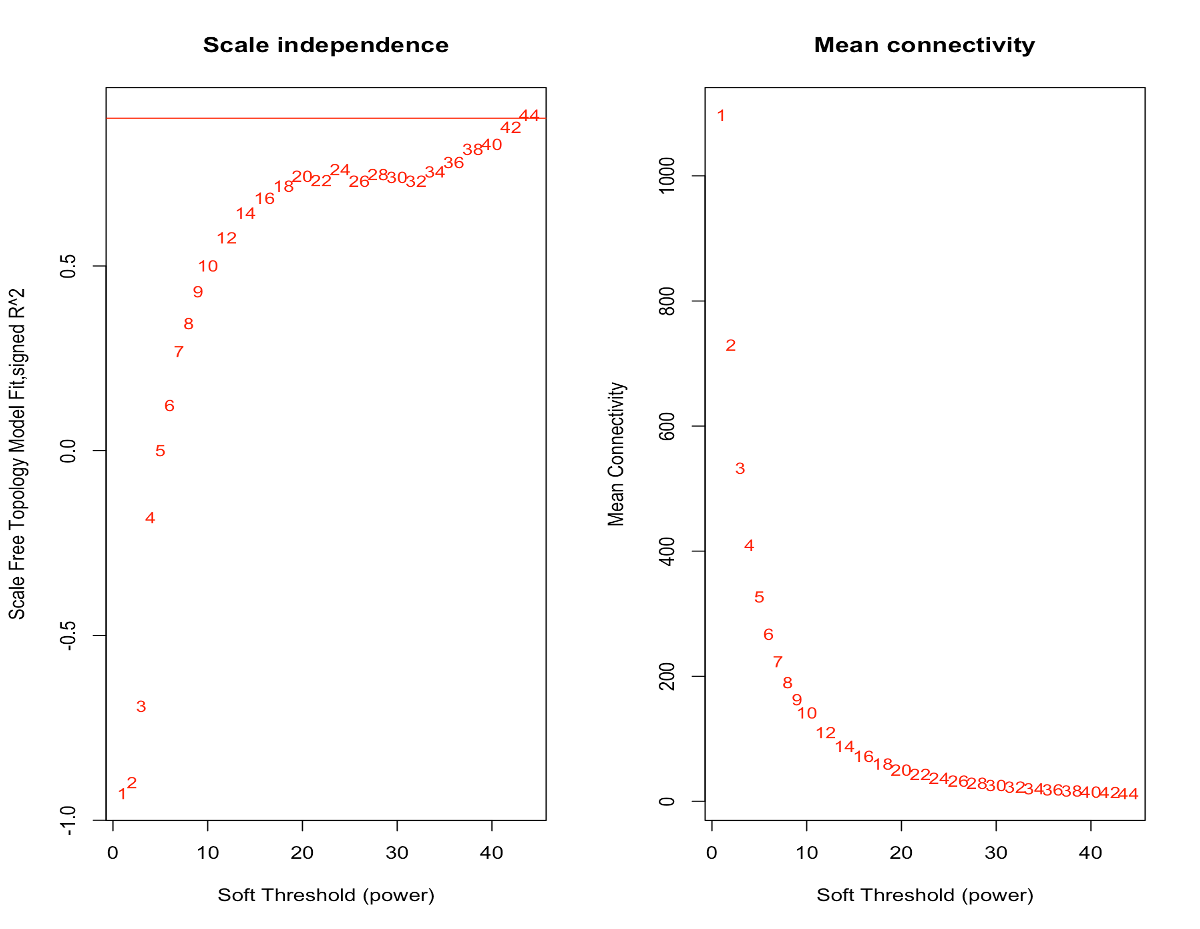
Thank for your good description. I know that in pickSoftThreshhold function, we can test different power as input by some parameter. for example, for my new analysis, I get below results:
Power SFT.R.sq slope truncated.R.sq mean.k. median.k. max.k.
1 1 0.365 -3.23 0.959 4480.000 4.36e+03 7630.0
2 2 0.673 -3.15 0.980 1060.000 9.77e+02 2940.0
3 3 0.792 -3.04 0.990 325.000 2.74e+02 1390.0
4 4 0.835 -2.94 0.993 119.000 8.92e+01 751.0
5 5 0.841 -2.83 0.988 49.500 3.23e+01 443.0
6 6 0.849 -2.58 0.972 23.100 1.28e+01 279.0
7 7 0.942 -2.13 0.990 11.900 5.46e+00 185.0
8 8 0.957 -2.05 0.993 6.600 2.49e+00 151.0
9 9 0.970 -1.94 0.992 3.950 1.20e+00 128.0
10 10 0.965 -1.85 0.983 2.510 6.07e-01 110.0
11 12 0.965 -1.67 0.980 1.190 1.74e-01 84.9
12 14 0.962 -1.56 0.981 0.654 5.64e-02 67.5
13 16 0.962 -1.48 0.983 0.403 1.98e-02 54.8
14 18 0.962 -1.42 0.984 0.269 7.42e-03 45.3
15 20 0.939 -1.39 0.963 0.189 2.94e-03 38.0
based on ablin() function for finding an R^2 cut-off of h, now as you can see in 2 links below, no power intersect by "red" line. line above power = 6 and below power = 7. By which criteria or criterias I can get enough insight for finding good soft threshold value?
I appreciate if you share your comment with me.
Best Regards,
https://www.dropbox.com/s/0jiv3g94my8fa2f/Rplot--Scale%20independence-SelectionFilter-970916.pdf?dl=0
https://www.dropbox.com/s/6famodxb4674hb1/Rplot--Mean_Connectivity-SelectionFilter-970916.pdf?dl=0
Here, I would choose a value of 7