I am performing a differential expression analysis using DESeq2 of a dataset that have a batch effect due to a technical variable.
I am performing the differential expression analysis with two approaches:
Approach 1: considering the technical variable as covariate in the building of the dds model
Approach 2: Not considering the technical variable as covariate.
I obtained two lists of genes differentially expressed.
I was wondering if it is correct to compare the two list of genes and consider the more significant genes (TRUE positives) the genes that are identified by both approaches.
No, those genes would be the ones for which the batch effect doesn't matter. The real question you should be answering is if you need to control for the batch effects or not, which can be a complicated question. You could check a PCA plot to see if there is any evidence for a strong batch effect. In addition, you can plot a histogram of the p-values for the models with and without the batch effect (here you are plotting the p-values for the coefficient of interest). Normally you should get a flat histogram with a peak on the left side. That's the expectation because under the null you expect the p-value histogram to be uniform, so for most of the genes this should be true, and you should have a flat histogram. But for some (the non-null genes) you expect p-values that are smaller than expected under the null, so you get the peak at the left.
A hallmark of a model with unaccounted confounders is a histogram that goes down at the left. So if we describe it from right to left, it's flat, then it starts going up, but then it goes back down again. That's what it looks like when you are biased towards the null, which is what often happens when you have unaccounted confounders like a batch effect. Anyway, I would base the choice on the PCA plot and the p-value histograms rather than the list of genes.
Thank you for your reply. I have some more questions.
If I have a batch effect in my dataset, should I always take into account it in my differential expression analysis? What will happen if I do not consider the technical variable?
I have plotted the histogram of the p-values considering and not considering the batch effect. I obtained that without considering the technical variable I have a pick on the right of the plot and it goes down at the left side. When I considered the technical variable as covariate I obtained a pick on the right of the plot (at p-value =1) then it goes down toward the left side and I got a second pick on the left side (at p-value=0.0). In addition, the pick on the right is greater than the pick on the left of the plot. I was wondering if this bimodal distribution suggests that there is still a unaccounted confounders in the dataset.
I also considered another possible variable in my differential expression analysis and I obtained that after considering this variable the plot of the p-value still have the bimodal distribution but the right pick is smaller than the left pick (opposite distribution compared to the previous correction). Does this indicate that the second variable could be the real confounders variable?
If you have a true batch effect, you always have to take it into account. Otherwise, your results will likely be biased towards the null. Having a peak on the right side of the p-value histogram probably means you haven't done a good job of filtering out genes with extremely low (or all zero) counts. See the DESeq2 vignette for an example.
I added the filtering of low counts genes in my pipeline and now I do not have the pick on the right side of the plot.
I noticed that when I considered one variable as technical variable instead of another the number of genes having a pick in the left side change.
Does the variable with the greatest pick at the left side is the true confounders variable?
I attached a picture with the different distributions.
Your questions have moved from generalities about analyzing data to specifics about your data. At this point it's up to you as the analyst to decide what variables make sense in the context of your study.
OK! Thank you. So if I understood well the higher pick in the left part of the plot does not indicate from the technical point of view that the variable is the real variable that confound the experiment.
No, the height of the peak simply tells you how many genes have small p-values, given the model you fit. The two histograms on the right both look OK to me, but I don't know anything about your experiment or what variable 1 and variable 2 are.
The p-value histogram is really only useful to find grossly mis-specified models, and neither the single variable nor the two variables look mis-specified.
Hi!
Thank you for your reply. I have some more questions.
If I have a batch effect in my dataset, should I always take into account it in my differential expression analysis? What will happen if I do not consider the technical variable?
I have plotted the histogram of the p-values considering and not considering the batch effect. I obtained that without considering the technical variable I have a pick on the right of the plot and it goes down at the left side. When I considered the technical variable as covariate I obtained a pick on the right of the plot (at p-value =1) then it goes down toward the left side and I got a second pick on the left side (at p-value=0.0). In addition, the pick on the right is greater than the pick on the left of the plot. I was wondering if this bimodal distribution suggests that there is still a unaccounted confounders in the dataset.
I also considered another possible variable in my differential expression analysis and I obtained that after considering this variable the plot of the p-value still have the bimodal distribution but the right pick is smaller than the left pick (opposite distribution compared to the previous correction). Does this indicate that the second variable could be the real confounders variable?
Thank you.
Concetta
If you have a true batch effect, you always have to take it into account. Otherwise, your results will likely be biased towards the null. Having a peak on the right side of the p-value histogram probably means you haven't done a good job of filtering out genes with extremely low (or all zero) counts. See the DESeq2 vignette for an example.
I added the filtering of low counts genes in my pipeline and now I do not have the pick on the right side of the plot.
I noticed that when I considered one variable as technical variable instead of another the number of genes having a pick in the left side change. Does the variable with the greatest pick at the left side is the true confounders variable?
I attached a picture with the different distributions.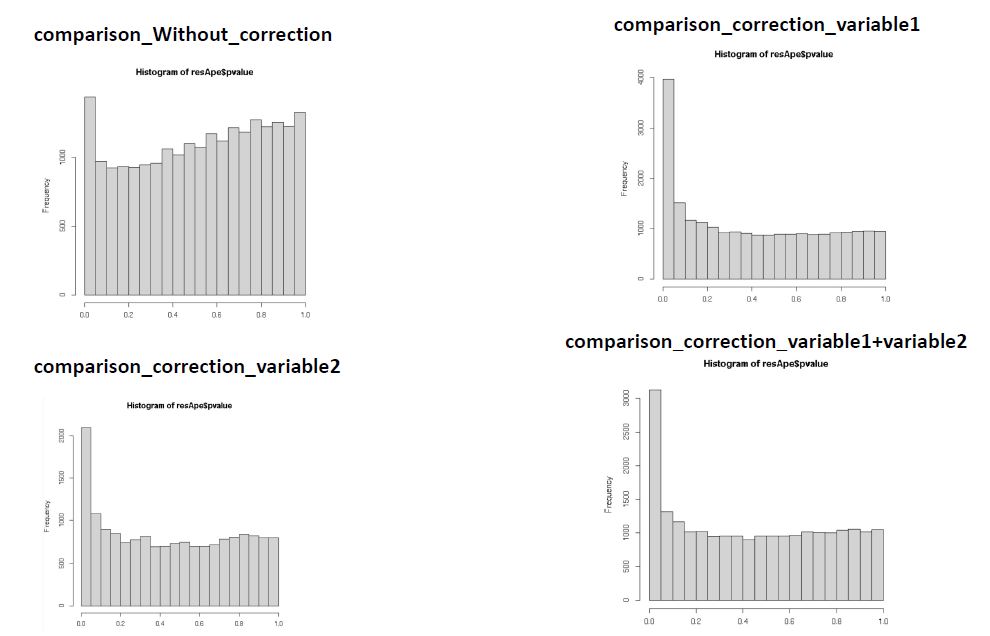
Your questions have moved from generalities about analyzing data to specifics about your data. At this point it's up to you as the analyst to decide what variables make sense in the context of your study.
OK! Thank you. So if I understood well the higher pick in the left part of the plot does not indicate from the technical point of view that the variable is the real variable that confound the experiment.
No, the height of the peak simply tells you how many genes have small p-values, given the model you fit. The two histograms on the right both look OK to me, but I don't know anything about your experiment or what variable 1 and variable 2 are.
The p-value histogram is really only useful to find grossly mis-specified models, and neither the single variable nor the two variables look mis-specified.