Question

The correlation between normalized counts and TPM based on 2-factor analysis by DESeq2

0

Entering edit mode

hequn • 0

@3c7c0ace

Last seen 3.5 years ago

France

Enter the body of text here Hello everyone,

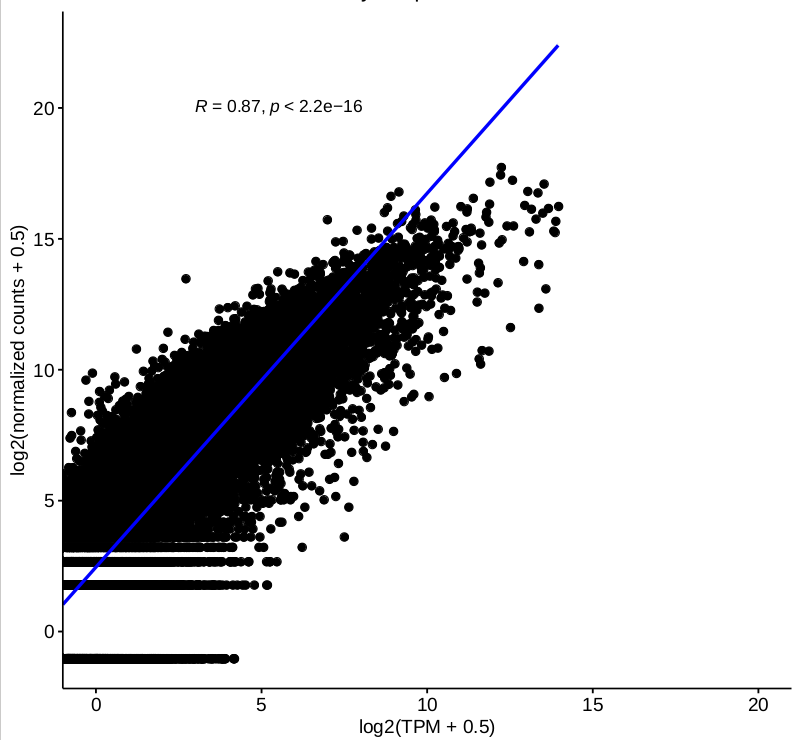
I have some questions about DESeq2 2-factor analysis. One of our ongoing project is about RNA-seq data from patient and control (2 genotypes) with or without stimulation(not stimulation, stimulation 1 and 2, 3 conditions in total), for each sample, we have different number of technical replicates, and we are very interested in interaction between genotype and condition. I tried to carry on my analysis by 2-factor mode using DESeq2 with design ~ condition + genotype + condition:genotype with collapsing the technical replicates firstly. The “results” function was used to extract individual interaction term(element from resultsNames(object)) from object has been called by DESeq. Some top DEGs were selected to do visualization by “plotcounts” function, and we found that normalized counts for some genes are not consistent with their TPM. Then we checked the correlations between log-transformed TPM and normalized counts based on 2-factor, and the correlation for single sample based on expressed genes is good

(figure 1) Figure 1. The correlation between normalized counts and TPM for single sample

while the correlation for the ratio of each group, for example, correlation of log( normalized counts of (patient-stimulation 1/ctrl-stimulation 1) ) and log( TPM (patient-stimulation 1/ctrl-stimulation 1) ), based on 2-factor mode is not good

(figure 2)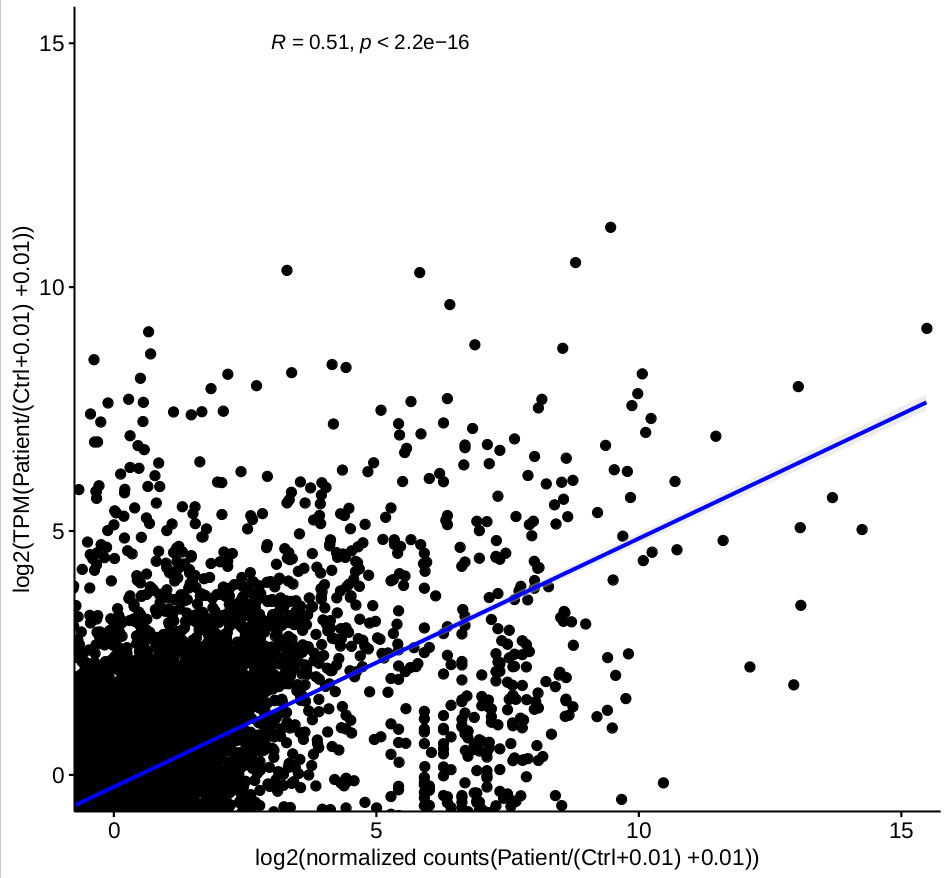 Figure 1. The correlation between normalized counts and TPM for the ration of each group .

Do you how to explain this question? Do I need to take some action to correct the normalization based on two factor?

Thank you in advance.

Code should be placed in three backticks as shown below


# include your problematic code here with any corresponding output 
# please also include the results of running the following in an R session 

sessionInfo( )

DESeq2 RNASeq • 2.8k views

ADD COMMENT • link 3.6 years ago hequn • 0

1

Entering edit mode

How did you compute TPMs? In what ways were the results vastly different? That TPMs and normalized counts don't fully correlate isn't surprising, there's a reason TPMs aren't used for statistics.

ADD REPLY • link 3.6 years ago dpryan79 ▴ 10

0

Entering edit mode

Thank you so much for you response.

TPM is calculated by the company, I do not know which software they used to generate them. I had used kallisto to produce TPMs before. The difference is that the correlation between the ratio of normalized counts and TPM are very good based on one-factor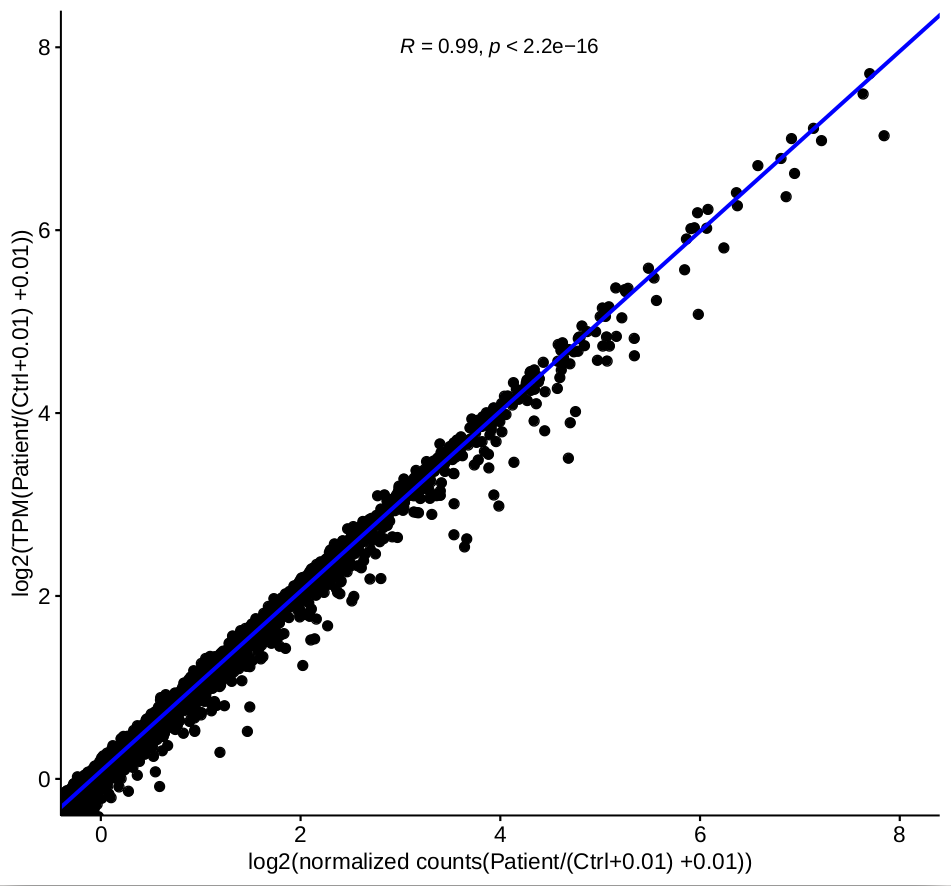 as shown in figure 3.

ADD REPLY • link 3.6 years ago hequn • 0

0

Entering edit mode

Could you post your code where you make these plots?

ADD REPLY • link 3.6 years ago Michael Love 43k

0

Entering edit mode

This is the code for figure 1

normalized_counts = as.data.frame(counts(dds, normalized = TRUE))
normalized_counts$ID = rownames(normalized_counts)
TPM = read.csv("TPM.csv")
rownames(TPM) = TPM$X
TPM = TPM[,-c(1,8,13)]
TPM$ID = rownames(TPM)
normlized_counts.TPM = merge(TPM, normalized_counts, by.x = "ID", by.y = "ID")
rownames(normlized_counts.TPM) = normlized_counts.TPM$ID
normlized_counts.TPM = normlized_counts.TPM[,-1]

normlized_counts.TPM.log = log2(normlized_counts.TPM + 0.5 )

ggscatter(normlized_counts.TPM.log, x = "TPM", y = "normalizd counts", 
      add = "reg.line", conf.int = TRUE, 
      cor.method = "pearson",
      title = "Correlation between TPM and normalized counts for C21 sample two factor",
      xlab = "log2(TPM + 0.5)", ylab = "log2(normalized counts + 0.5)", xlim = c(0, 20),
      add.params = list(color = "blue", fill = "lightgray")) +
stat_cor(method = "pearson", label.x = 3, label.y = 20)

This code for figure 2

  tpm_2.vs.5.two.factor.TPM = merge(res.2.vs.5.two.factor.norm.counts, TPM, by.x = "ID", by.y = "ID")
  tpm_2.vs.5.two.factor.TPM[,2:ncol(tpm_2.vs.5.two.factor.TPM)] = apply(tpm_2.vs.5.two.factor.TPM[,2:ncol(tpm_2.vs.5.two.factor.TPM)], 
                                                                  2, as.numeric)
  tpm_2.vs.5.two.factor.TPM$log.2.vs.5.two.factor = log2(
         (((tpm_2.vs.5.two.factor.TPM[,"H180_A_stimulate.collapse"] + tpm_2.vs.5.two.factor.TPM[,"H226_A_stimulate.collapse"] ) )/2)/
         (((tpm_2.vs.5.two.factor.TPM[,"C21_A_stimulate.collapse"] + tpm_2.vs.5.two.factor.TPM[,"C64_A_stimulate.collapse"] + tpm_2.vs.5.two.factor.TPM[,"C96_A_stimulate.collapse"]) )/3 + 0.01) + 0.01

) tpm_2.vs.5.two.factor.TPM$log.2.vs.5.TPM = log2( (((tpm_2.vs.5.two.factor.TPM[,"L.collapse"] + tpm_2.vs.5.two.factor.TPM[,"M.collapse"] ) )/2)/ (((tpm_2.vs.5.two.factor.TPM[,"D.collapse"] + tpm_2.vs.5.two.factor.TPM[,"E.collapse"] + tpm_2.vs.5.two.factor.TPM[,"F.collapse"]) )/3 + 0.01) + 0.01
)

ggscatter(tpm_2.vs.5.two.factor.TPM, x = "normalized.counts", y = "TPM", 
      add = "reg.line", conf.int = TRUE, 
      #cor.coef = TRUE, 
      cor.method = "pearson",
      title = "Correlation between log(Patient-A / Ctrl-A) two factor \nVS log(Patient-A / Ctrl-A) TPM",
      xlab = "log2(normalized counts(Patient/(Ctrl+0.01) +0.01))", ylab = "log2(TPM(Patient/(Ctrl+0.01) +0.01))", 
      xlim = c(0, 15), ylim = c(0, 15), 
      add.params = list(color = "blue", fill = "lightgray")) +
stat_cor(method = "pearson", label.x = 3, label.y = 15)

ADD REPLY • link 3.6 years ago hequn • 0

score 0 · Answer 1 · 2021-04-22

0

Entering edit mode

Michael Love 43k

@mikelove

Last seen 1 day ago

United States

My first guess is that there is a bug in the merging code. I don't see anything in particular, but you've got a lot of code and whereas things are tightly linked in DESeq2 functions, there could have been a slip in the merging or construction of LFCs.

But in general, the LFC using counts take into account precision of the data, so won't be correlated with r=1 if you do something manually with TPMs.

ADD COMMENT • link 3.6 years ago Michael Love 43k

0

Entering edit mode

Thank you very much for your reply. I agree with you, what I do not understand is that the correlation by one-factor mode seems good but not good for two-factor.

ADD REPLY • link 3.6 years ago hequn • 0