Hi everyone,

I understand that when performing differential analysis between different groups using limma, it is better to include all samples and using contrasts rather than subsetting the groups to better estimate the variance.

However, I have a complex design where this is causing me an issue.

For context, I am performing differential methylation analysis between 3 groups. This is a reduced example dataset of my analysis with my study design (I have a larger dataset and observing the same issue described here) :

df = structure(list(Group = c("G1", "G2", "G1", "G2", "G2", "G1", 
                              "G3", "G3", "G3", "G3", "G3", "G3", "G3"), V1 = c(36L, 36L, 26L, 
                                                                                26L, 34L, 34L, 40L, 29L, 34L, 31L, 34L, 35L, 25L), V2 = c("Covar1", 
                                                                                                                                          "Covar1", "Covar1", "Covar1", "Covar2", "Covar2", "Covar2", "Covar3", 
                                                                                                                                          "Covar1", "Covar2", "Covar2", "Covar2", "Covar1"), Subject = structure(c(3L, 
                                                                                                                                                                                                                   3L, 6L, 6L, 7L, 7L, 1L, 2L, 4L, 5L, 8L, 9L, 10L), levels = c("1", 
                                                                                                                                                                                                                                                                                "2", "3", "4", "6", "8", "13", "16", "18", "23"), class = "factor")), row.names = c(NA, 
                                                                                                                                                                                                                                                                                                                                                                    -13L), class = "data.frame")

design <- model.matrix(~0+Group+V1+V2+Subject, data=df)

beta_test <- c(0.598403375449404, 0.635837157363606, 0.577366021553369, 0.614350852641186, 
               0.979187240034327, 0.964493441174273, 0.976979399329944, 0.976636922254339, 
               0.973782723774806, 0.979580729724208, 0.971783039226741, 0.0381216484812949, 
               0.647705918700804)

fit <- lmFit(beta_test, design)
contr <- makeContrasts(GroupG2 - GroupG3, levels = colnames(coef(fit)))
fit2 <- contrasts.fit(fit, contr)
fit2 <- eBayes(fit2)

degrees.freedom = fit2$df.residual - 1
DMPs=data.frame(effectsize=fit2$coefficients,SE=fit2$stdev.unscaled*fit2$sigma,Pval=fit2$p.value,degrees.freedom=degrees.freedom)
DMPs$probe=rownames(DMPs)
colnames(DMPs)=c("effectsize",'SE',"Pval","degrees.freedom","probe")
DMPs

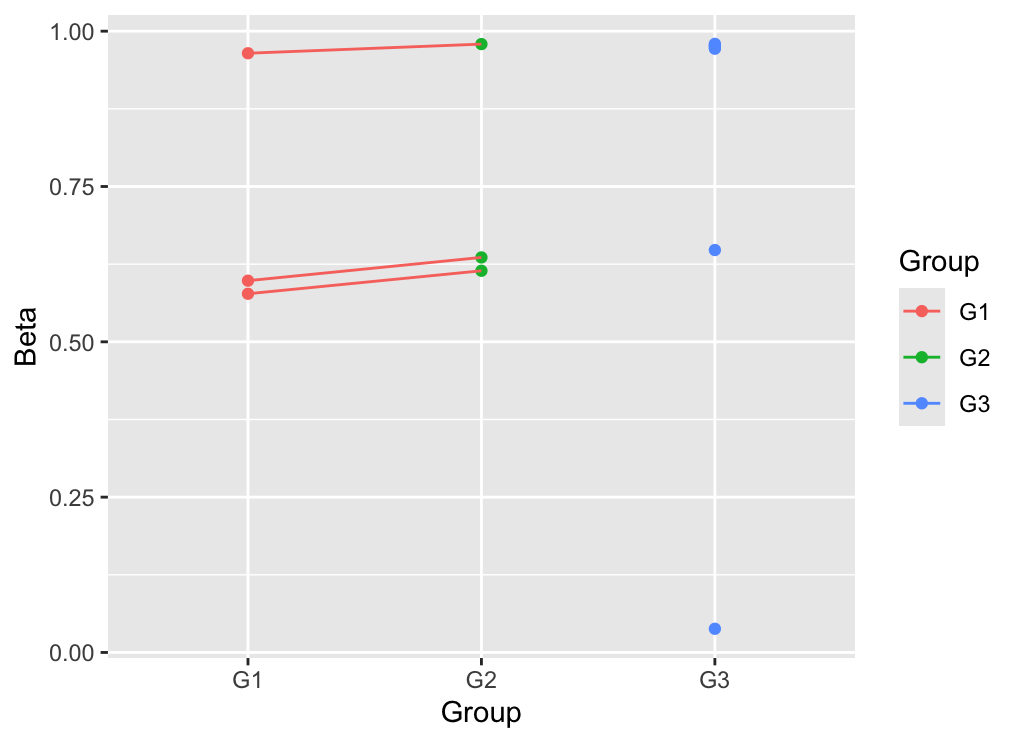
So I have 3 groups, with 3 covariates that I want to adjust in my model (V1,V2, Subject). For 2 groups (G1/G2), samples are paired (coming from the same individual) while the remaining group (G3) are samples from other individuals. I use contrasts to compare G1, G2 and G3 but when comparing G3 vs. G1 and G3 vs. G2, I have a problem with effect sizes. Indeed my data are beta values that ranges between 0 and 1 (I know it is not optimal here). However, the effect size announced by the G3 vs. G1 here is 1.13 which is not reliable.

When I remove the Subject covariate in the design, the effect size is 0.03 which is more logical when looking at the data.

I am sorry as my knowledge is limited in statistics and my question may be pointless, but why is there such a huge variation between both models while there is not a big effect of Subject according to the plot (dots that are connected are from the same subject)?

Is it ok to perform the analysis without the Subject for G3 vs. G1 and G3 vs. G2 but keeping the Subject for G2 vs. G1 and thus changing the design while comparing the groups ?

Thank you in advance for your help

The design matrix is over-parametrized by including too many covariates. It is not correct to include patient covariates in the model as well as the patient effect itself, and the results that you get from such an overparametrized model are not meaningful. edgeR would give an error with this design matrix. limma gives a warning rather than an error, but this is still a situation that you need to avoid.

You need to remove the covariates. If you do so, then it will not make any difference whether the G3 samples are included or not.

You asked a question four years ago with a very similar experimental design: Complex design with paired and unpaired samples with edgeR RNA-seq DE analysis. In both cases the first two groups are paired but the third is not. My answer from four years ago would still apply here.