Yesterday I became enamored by the following paper. It claims that one can massively improve an RNA-Seq analysis by simply removing 5-20 counts from every sample.
- Modeling and cleaning RNA-seq data significantly improve detection of differentially expressed genes BMC Bioinformatics, 16 November 2022
As I read, it struck me as potentially very ingenious or very wrong. I could not decide which one was true. It also seems like a very simple approach.
The method estimates the random error from very low counts and subtracts that value uniformly over the sample.
The complexity of the method is extraordinarily low - it may be written out in perhaps a dozen lines of code in R. That being said, their R implementation is incorrect - in my opinion - within just a few lines, it has several bugs not to mention a quite ad-hoc approach to solving the problem
https://github.com/Deyneko/RNAdeNoise
So the code above does not quite do what it claims - other than actually removing a low number of counts.
But they still claimed to observe that the method is effective: the authors claimed that they are getting larger, and I mean a substantially larger number of DE genes with both edgerR and DeSeq2.
So I kept trying to reproduce it out of sheer curiosity.
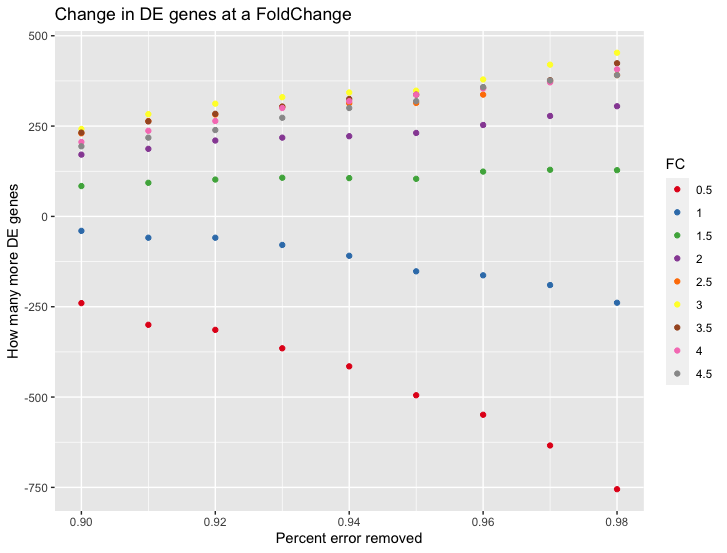
I reimplemented the method - correctly this time - the way I think the method should work - and ran it myself (on the input data the authors provided). And I, too, do get more DE genes (while running edgeR), substantially so. I am quite surprised by just how many more DE genes it produces.
It works for high foldchanges and not low-fold changes, which also boggles my mind - as I expected it the other way around;
Here is the benchmark I ran with my code, it shows How many more DE genes one would get if at each different Fold Change if we subtract an increasing number of counts (the values end being between 4-30) from each sample.
So my question: Is this a valid approach going forward?


Hello Gordon; thank you for the advice,
I deliberately did not provide code because I felt the principle is what is under discussion and that by providing data, I would only make the problem overspecified. There could be bugs in my code, the data I choose could be peculiar, etc., and all that would do is divert the attention from the big picture.
The paper's main claim is that in typical RNA-Seq experiments, most of the low counts are all due to errors (from an exponential function). And that reducing all counts by N is beneficial as it removes more errors than true data. It does not even matter how big that N is (magnitudes seem to range from 5 to 20)
We don't even need to figure out the precise value of N. Reducing our counts by 1 would also work; if the most likely counting error per gene was N before, we now made it smaller it is N-1; provided the approach is valid. I am looking for feedback on whether this intuitively makes sense and sounds valid.
The main claim of the paper could be distilled down to the following bare minimal statement:
In realistic scenarios, you should subtract at least 1 from your counts (set negative counts back to 0). This subtraction will generally remove the error component from the counts. Running a statistical method on these corrected counts will generate better results.
This principle above is the question I am trying to answer here whether it makes sense at the conceptual level. Does it raise any flags, or does it sound plausible?
The reason my interest is so piqued is not that it might potentially work (it is not my main motivation in following up on this).
My main motivator is that the proposed solution appears to be both: extraordinarily simple and counterintuitive simultaneously. And how come I can't decide with a single glance whether universally subtracting 1 is a good idea or a bad one?
The method you describe in your comment does not sound remotely plausible to me. The idea that errors in RNA-seq counts are additive and that you can subtract them out seems quite fanciful. I can easily think of scenarios where subtracting counts in this way would cause spurious DE, or destroy genuine DE, or even reverse the direction of change.
It's hardly surprising that the authors would get more DE from their method compared to analysing raw counts. That is because they are judging DE mainly by fold-change instead of by p-value, and the subtraction method artificially increases fold-changes.
Ironically, the authors could have got even more DE had they simply used edgeR as recommended instead of applying an arbitrary fold-change cutoff.
The idea of subtracting background from observations has been proposed a million times in different contexts. It is a method much beloved by engineers. Unfortunately, naive subtraction is almost always statistically horrible. It was one of the prevailing ideas we had to combat in microarray data analysis more than 20 years ago. I must say it makes even less sense in the RNA-seq context.
Oh indeed! I consider myself an engineer at heart! This might be a reason of why the method appealed to me so much in the first place.
Thank you for the insights and context!
Doesn't it bother you that the paper proposed to subtract the same value from every count regardless of sequencing depth? Failure to account for differences in sequencing depth between different samples in the same dataset seems a pretty serious danger flag to me.